Work hardening in colloidal crystals

The properties of atomic crystals under high strain are well established¹⁸; when subjected to stresses beyond the yield stress, they exhibit plastic flow, which causes an irreversible change in their shape. This is mediated by nucleation and motion of topological line defects called dislocations^18,23. Increasing plastic deformation requires an increasing flow stress because of the interactions between dislocations. This is work, or strain, hardening. This phenomenon is ubiquitous, yet, owing to the many ways dislocations can interact, our understanding of the mechanism that governs work hardening is still incomplete^{20,22,24,25,26}. In contrast to atomic crystals, colloidal crystals have much simpler interparticle interactions; they consist of solid particles in a fluid and can exhibit purely hard-sphere interactions. Here we show that, despite the simplicity of these interactions, hard-sphere colloidal crystals exhibit work hardening. The micron scale of the particles enables the structure and dynamics of colloidal crystals to be investigated on a particle-by-particle level using optical microscopy^{5,8,9,12,13,14,27,28,29}. Dislocations in these colloidal crystals can, therefore, be directly visualized in three dimensions and in real time. Thus, these measurements provide insight into the general nature of work hardening.

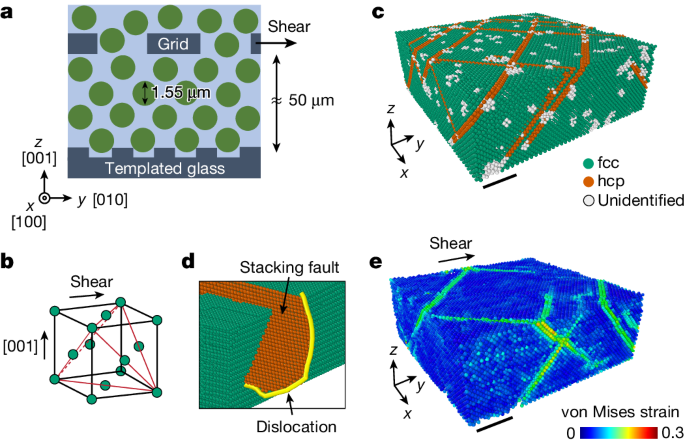
We disperse 1.55 μm diameter silica spheres in a mixture of water and dimethyl sulfoxide, which closely matches the refractive index of silica. We dissolve a small amount of fluorescein sodium salt to dye the solvent and additional sodium chloride to further screen the surface charge of the particle to produce a nearly hard-sphere interaction between the particles. The colloidal dispersion is put into a cylindrical shear cell, 1 cm in diameter. The bottom of the cell is a template: a coverslip with a square array of dimples of 1.63 μm spacing (Fig. 1a). The template constrains the first layer of the sedimenting particles and imposes the growth of a face-centred cubic (fcc) single crystal along the [001] fcc direction³⁰ (Fig. 1b). We use a spinning-disk confocal microscope to image, at single-particle resolution, five separate regions of 200 × 200 × 60 μm³ volume, containing a total of about 5 million particles (Extended Data Fig. 1 and Supplementary Videos 1–3). By processing the confocal images, we locate the position of the particles in three dimensions, which allows us to determine the local crystalline structure³¹ and reconstruct the dislocation lines³² with their respective Burgers vectors, b.

a, Schematic of the experiment. Colloidal crystals are grown by sedimentation of 1.55 μm particles on templates with a square pattern of dimples. The templates dictate the growth of fcc single crystals along the [001] fcc direction. The crystals are sheared by displacing a grid, embedded in the particles, in the [010] fcc direction. b, The four close-packed {111} planes are marked in the fcc unit cell. c, During the sedimentation process, the hcp stacking faults (orange) in the fcc crystal (green) are formed on the four {111} planes. d, The stacking faults arise because of the motion of Shockley partial dislocations (yellow line in d) that relax the approximately 1% misfit strain due to the mismatch between the template spacing and the crystal lattice constant. e, A snapshot of the von Mises equivalent strain, calculated for γ ≈ 0.04 with respect to a reference frame defined at γ = 0. Plastic flow is mediated by slip on the {111} fcc planes, the classical easy-glide planes, as shown by the high von Mises strain values (Supplementary Video 5). c and e correspond to the same region of the crystal. Scale bar, 20 μm (c,e).

The as-grown fcc crystals contain multiple stacking faults, characterized by local hexagonal close-packed (hcp) stacking, that lie on the {111} planes, as shown by the orange particles in Fig. 1c. Stacking faults are bounded by Shockley partial dislocations (Fig. 1d) and are formed during the growth of the crystal as a result of the approximately 1% misfit strain between the crystal and the template¹¹ (Supplementary Video 4). After the particles have fully sedimented, we shear the crystal by displacing a square-meshed grid, embedded 50 μm above the template, as shown schematically in Fig. 1a. The grid moves in the [010] fcc direction at a constant speed of 2.5 μm h⁻¹, resulting in a strain rate of 1.4 × 10⁻⁵ s⁻¹ (Methods and Extended Data Fig. 2). During the deformation process, three-dimensional (3D) confocal scans are made every 4 min, fast enough to determine the time-dependent trajectories of the individual particles.

To quantify the deformation of the sheared crystal, we determine the elastic and total strain fields. The elastic strains are obtained for each snapshot of the particle positions by comparing the local particle configuration with the perfect fcc structure^12,33,34. By contrast, the total strains are defined with respect to the position of the particles before the deformation³³, which requires tracking the particle positions in time (Methods). The average elastic (γ_E) and total (γ) shear strains are obtained by averaging over all the particles. Here, γ is equivalent to the relative displacement of the particles at the top and bottom surfaces divided by its height (Extended Data Fig. 3).

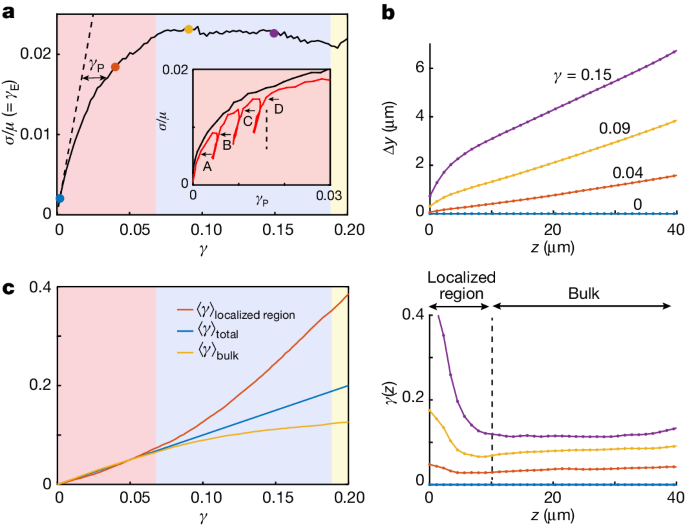
We find that the deformation of the crystal is elastic up to γ ≈ 0.005; the total strain is accommodated by elastic strain, γ_E = γ, as shown in Fig. 2a by the dashed line with a slope of 1. Beyond this yield point, any further increase in the imposed γ causes an increase in the plastic strain, γ_P = γ − γ_E. To determine how γ_P is accommodated by the crystal, we calculate the spatially resolved von Mises equivalent strain, a scalar invariant that quantifies the maximal shear distortion (Methods). Plastic strain is mediated by slip along the oblique {111} planes, as shown by the high von Mises strain values in Fig. 1e. These measurements show that plastic strain is mediated by the classic fcc slip on the close-packed planes.

a, The normalized shear stress σ/μ, where μ is the shear modulus, is obtained from the measurements of the elastic strain, γ_E, and plotted as a function of the total strain, γ. The dashed line with a slope of unity marks elastic deformation, γ_E = γ. The plastic strain, γ_P = γ − γ_E, is denoted by the black double arrow. Inset, strain hardening is demonstrated by replotting σ/μ as a function of γ_P (black line); increasing stresses are required to sustain plastic flow. Successive unloading and reloading (red line) demonstrate the irreversibility of the plastic flow; the yield stress, the stress at which the slope dσ/dγ_P suddenly decreases, increases with accumulated γ_P (A–D). b, Profiles of the average particle displacements (top) in the direction of the shear, y, binned along the crystal height, z, for different values of γ (coloured dots in a). The corresponding profiles of γ (bottom) demonstrate that, at the later stages of the deformation, the strain is localized within a narrow region. c, Strains, averaged over the localized region (red line), the bulk region (yellow line) and over the total thickness (blue line), as defined in b (bottom). During the strain-hardening regime (red background in a,c), the crystals are deformed homogeneously. Saturation of the stress marks the onset of a crossover between the homogenous and localized flow regimes (blue background in a,c). The deformation of the bulk stops entirely at γ ≈ 0.2, and the strain is accommodated in the localized region alone (yellow background in a,c).

The average elastic strains provide a measure of the normalized stresses σ/μ = γ_E, where μ is the shear modulus. Remarkably, our experiments show strain hardening in these hard-sphere colloidal crystals: increasing stresses are required to accommodate plastic flow, as seen by plotting σ/μ as a function of γ_P, shown by the black line in Fig. 2a (inset). To demonstrate the irreversibility of the plastic flow, we reverse the direction of the shear to remove part of the applied shear stress, and then reload. We find that higher stresses are required to reinitiate plastic deformation: the yield stress, the point at which the slope dσ/dγ_P suddenly decreases, increases with the accumulated γ_P, as denoted by the capital letters (A–D) in Fig. 2a inset. Although the transition to yield is clear, the unloading and reloading stages are not purely elastic, which would require the loading and unloading curves to be strictly vertical (Fig. 2a, dashed line in the inset).

The strain-hardening stage ends when the stress reaches σ/μ ≈ 0.02 (Extended Data Fig. 4). Any further flow is maintained at a constant stress level (Fig. 2a). The saturation of stress marks an essential change in the behaviour of the flow. To demonstrate this, we average the particle displacements in the shear direction over the crystalline layers parallel to the substrate. Before the saturation of the stress, the entire crystal undergoes simple shear: the displacement profile is linear, and the strain profile is constant across the thickness of the crystal, as demonstrated by the orange profiles in Fig. 2b. However, during the later stages of the deformation, when the stress saturates, strong displacement gradients near the bottom surface are formed, as shown by the yellow and purple profiles in Fig. 2b (top). The deformation of the crystal is no longer homogeneous, and the strain becomes localized within a 10-μm thick boundary layer at the bottom surface (Fig. 2b, bottom).

To quantify the crossover between the homogenous and localized flow regimes, we average the strain within two separate regions of the crystal: the region in which localization takes place, 0 < z < 10 μm, and the bulk of the crystal, in which the deformation is homogenous, 10 μm < z < 40 μm. We find that during the strain-hardening stage (red background in Fig. 2a,c), the two strain averages are identical, highlighting again that the deformation is homogeneous over the entire thickness of the crystal. The saturation of the stress, which marks the end of strain hardening, is accompanied by the onset of localization; strain in the localized region exceeds the bulk strain (blue background in Fig. 2a,c). Finally, when the bulk strain saturates, the applied strain is accommodated by the localized region alone (yellow background in Fig. 2a,c).

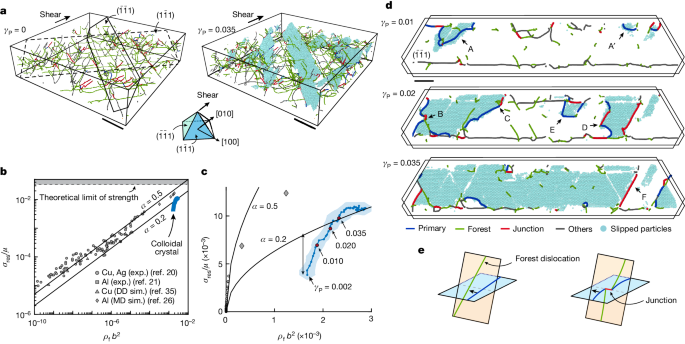
To explore the origin of strain hardening, we reconstruct the evolution of the full 3D dislocation network during the deformation process, as shown for γ_P = 0 (Fig. 3a, left) and γ_P = 0.035 (Fig. 3a, right). We find that slip is mediated predominantly by two slip systems (Methods and Extended Data Fig. 5): glide of \(\frac{1}{6}[2\bar{1}1]\) and \(\frac{1}{6}[21\bar{1}]\) Shockley dislocations on, respectively, \((\bar{1}\bar{1}1)\) and \((1\bar{1}1)\) planes (Fig. 3a). The two slip systems are symmetric with respect to the applied shear: we calculate the average the density of all the dislocations that pierce through the two slip planes, which defines the forest dislocation density ρ_f (Methods). We find that late-stage strain hardening in colloidal crystals is described by the Taylor equation, originally derived to explain strain hardening in atomic crystals¹⁹: to sustain dislocation glide, the shear stress resolved on a slip system σ_res (Methods) increases with ρ_f according to \({\sigma }_{{\rm{r}}{\rm{e}}{\rm{s}}}=\alpha \mu b\sqrt{{\rho }_{{\rm{f}}}}\), where α is a dimensionless constant and b is the magnitude of the Burgers vector²². Moreover, measurements of σ_res/μ and ρ_fb² in our colloidal crystals (blue symbols) are in accordance with experimental and numerical observations in metallic systems^20,21,26,35 (grey symbols) and the model predictions (black solid lines for α = 0.2 and 0.5) (ref. ³⁵), as shown in Fig. 3b. This result is particularly interesting given the four orders of magnitude difference in particle size (0.1 nm to 1 μm) and the nine orders of magnitude difference in the shear modulus (GPa to Pa) between metallic and colloidal crystals. Remarkably, the very dense dislocation network of our colloidal crystals leads to a very high σ_res/μ that exceeds that of most metals and ultimately approaches the theoretical limit of strength (Methods). A more detailed investigation of the data shows that the Taylor equation fails to account for the early stages of the strain-hardening regime. The initial dislocation density is the result of a slight tensile mismatch between the crystal and the template; thus, the Taylor equation overestimates the flow stress. Taylor hardening is established only after a transient evolution of the dislocation network (Fig. 3c).

a, Snapshots of the dislocation network before (left) and during (right) deformation. The particles displaced by the dominant slip system, \({\bf{b}}=\frac{1}{6}[2\bar{1}1]\) on the \((\bar{1}\bar{1}1)\) plane, are shown in cyan. Another slip system, symmetric with respect to the shear, operates on the \((1\bar{1}1)\) plane (dashed). b, Comparisons of the normalized shear stress resolved on the dominant slip systems, σ_res/μ (where μ is the shear modulus), as a function of the normalized dislocation density, ρ_fb² (where b is the magnitude of the Burgers vector) for a nearly hard-sphere colloidal crystal and various metallic crystals (Methods). The two solid lines are the predictions of the Taylor equation for two values of α (see main text). c, Data in b are on a linear scale. The double arrow denotes the discrepancy between the Taylor model and the colloidal crystals at the early stages of the deformation. d, A 5-μm thick slice of the (\(\bar{1}\bar{1}1\)) plane (solid line in a) is shown for different values of γ_P. At the early stages (γ_P = 0.01) crystals flow by nucleation of (half) loops of the dominant dislocations (blue segments. Examples are marked by A and A′). At the later stages (γ_P = 0.02), dislocations can form immobile junctions (red segments) by interaction with the forest dislocations (green segments, see definition in the text), as shown by examples B, C and D. Thereafter, plastic flow is accommodated by unzipping of the junctions (γ_P = 0.035), although new dislocations can still be formed (E). Some junctions are very strong and limit slip (F). For the complete time series, see Supplementary Video 6. e, Schematic showing how dislocations can intersect forest dislocations and form immobile dislocation junctions. Scale bars, 50 μm (a); 20 μm (d).

To gain insight into the mechanism of strain hardening, we examine the evolution of slip on a particular \(\left(\bar{1}\bar{1}1\right)\) plane, marked by the solid line in Fig. 3a. At early stages of the plastic flow (γ_P = 0.01), slip is mediated by nucleation of mobile dislocations (blue), as marked by A and A′ in Fig. 3d. We find that nucleation takes place at different parts of the crystal, either by formation of half loops at the vicinity of the upper surface of the crystal (examples A and A′) or by homogeneous nucleation of full dislocation loops within the bulk of the crystal (Extended Data Fig. 6). At the later stages of the flow, dislocations expand (γ_P = 0.02), and the slipped regions coalesce to cover the entire plane (γ_P = 0.035), as shown in Fig. 3d.

These observations reveal the underlying mechanism of Taylor hardening. At later stages of strain hardening (γ_P = 0.02), as the primary dislocations expand, they intersect with Shockley dislocations (Fig. 3e, forest, green) that lie on other glide planes and pierce through the primary plane²², as demonstrated by the schematics in Fig. 3e. We provide here direct experimental evidence that interactions between the primary and forest Shockley dislocations result in the formation of sessile junctions. Most of these junctions are of the Lomer–Cottrell type¹⁸ with \({\bf{b}}=\frac{1}{6}[10\bar{1}]\) (Extended Data Table 2), as shown by the red segments in examples B and D in Fig. 3d. However, we also identify Hirth-type junctions with \({\bf{b}}=\frac{1}{3}[0\bar{1}0]\), as occurs, for example, at C. We find that these dislocation junctions form strong obstacles to the motion of the mobile dislocations, as suggested by the high curvature of the primary dislocations pinned by the junctions³⁶ as in example B. Further plastic strain is accommodated by unzipping the immobile junctions (B, C and D). Our measurements show, however, a hierarchy of junction strengths, as some of the junctions remain intact (F), despite the increase in stress. These observations explicitly demonstrate the role of immobile junctions in strain hardening of crystals; to sustain plastic flow, the stress must be sufficiently high to overcome the pinning of dislocations.

Our measurements also show the origin of the discrepancy between the Taylor predictions and the measured flow stress, as observed at the early stages of the strain-hardening regime (Fig. 3c, double arrow). At low strains (γ_P = 0.01), the dislocations are short and do not interact with the piercing forest dislocations, so that no dislocation junctions have formed yet. Instead, our measurements suggest that the nucleation of dislocations is the dominant mechanism for strain hardening in this case. We find a hierarchy of barriers to dislocation nucleation; although some regions are susceptible to early nucleation at low stress (A and A′), nucleation can also take place at later stages of the flow and at higher stress (E).

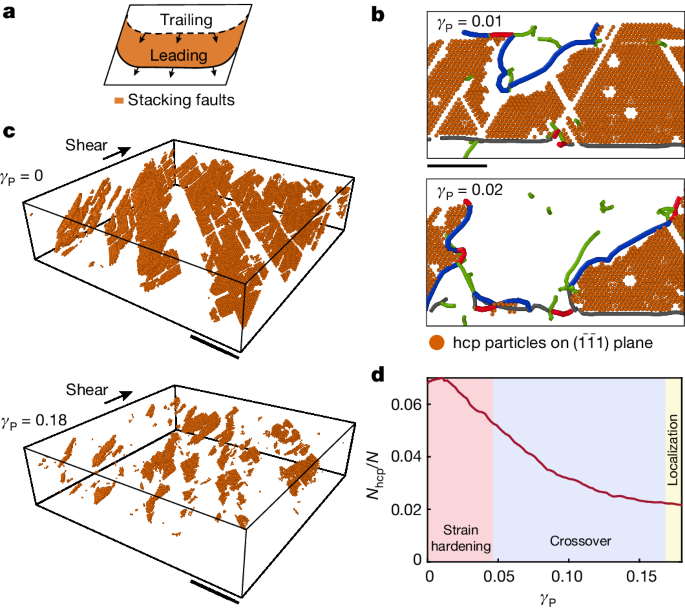
Strain hardening in our crystals is interrupted by the onset of localization. We find that the specific geometry of the Shockley partial dislocations limits the strain that can accumulate in the bulk. Unlike perfect dislocations, partial dislocations consist of two types²³: on applied shear, leading partial dislocations leave behind hcp stacking faults, whereas trailing partial dislocations eliminate the pre-existing stacking faults, as shown in Fig. 4a. We find that the dominant slip systems are of the trailing type. By nucleation and expansion, the \(\frac{1}{6}[2\bar{1}1]\) dislocations on the \((\bar{1}\bar{1}1)\) plane negate the pre-existing hcp stacking faults that were left behind by the misfit dislocations during the epitaxial crystal growth³⁷ (Fig. 4b). As the plastic flow proceeds, the stacking faults are exhausted, as demonstrated by the number of hcp particles on stacking faults on \((\bar{1}\bar{1}1)\) planes; there is a marked decrease between γ_P = 0 and 0.18 as shown in the two panels of Fig. 4c. We systematically quantify this process by tracking the fraction of the hcp particles on \((\bar{1}\bar{1}1)\) planes, N_hcp/N. These measurements show that the exhaustion of the stacking faults marks the end of the crossover; the deformation of the bulk entirely stops (Fig. 2b, bottom) when the dominant slip systems do not operate because N_hcp/N saturates at a low value (Fig. 4d, yellow region).

a, Glide of leading partial dislocations creates hcp stacking faults, whereas glide of trailing dislocations eliminates the stacking faults. b, A slice of a \((\bar{1}\bar{1}1)\) plane, corresponding to example A in Fig. 3d. The dominant dislocations (blue) are of the trailing type; \(\frac{1}{6}[21\bar{1}]\) dislocations eliminate hcp stacking faults (orange particles) that were left behind by the motion of the Shockley misfit dislocations formed during the epitaxial crystal growth. c, Stacking faults that lie on the dominant \((\bar{1}\bar{1}1)\) planes. Stacking faults that were formed before the deformation process (top) are exhausted by the time plastic flow reaches γ_P = 0.18 (bottom). The crystal was sliced in the range 10 < z < 40 μm. d, Evolution of the number of hcp particles on \((\bar{1}\bar{1}1)\) plane, N_hcp, shown in c, normalized by the total number of particles, N. The decrease of N_hcp/N to small values marks the end of the crossover to localization (blue background). Thereafter, bulk deformation stops entirely (yellow background). Scale bars, 20 μm (b); 50 μm (c).

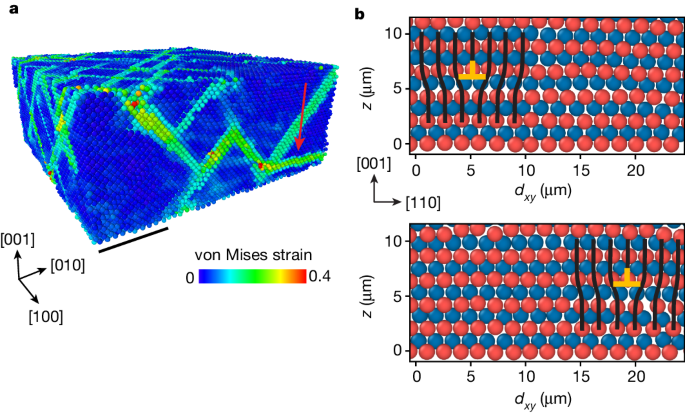
Finally, our measurements reveal the mechanism that drives the localization of flow. In contrast to the strain-hardening regime, during which slip occurs along the classic easy-glide {111} planes, flow localization is mediated by slip on an unconventional (001) slip plane, as demonstrated by the red arrow in Fig. 5a. Slip takes place through glide in the \([110]\) and \([1\bar{1}0]\) directions of Lomer dislocations^38,39,40, perfect dislocations of edge character in which \({\bf{b}}=\frac{1}{2}[110]\) and \(\frac{1}{2}[1\bar{1}0]\) (Fig. 5b). The presence of perfect dislocations in near-hard-sphere colloidal crystal is surprising. Perfect dislocations are expected to dissociate into partial dislocations because of the vanishingly small stacking fault energy. Here, as a result of the applied shear stress, mobile partial dislocations merge with the misfit dislocations to form perfect Lomer dislocations near the bottom interface. Lomer dislocations are often considered to be relatively immobile because of the high frictional forces on the (001) plane²³. Activation of Lomer dislocations in our experiments is a direct consequence of the severe work hardening of the {111} slip systems, which allows the activation of the less favourable (001) slip system. At this stage, the resolved flow stress is about 0.01μ as shown in Fig. 3b; this is close to the theoretical limit of strength and is reached in very few other materials.

a, A snapshot of the von Mises equivalent strain, calculated for γ ≈ 0.06, after the onset of the localization of flow. High values show that slip on an unconventional (001) plane has been activated (red arrow), apart from easier slip along the classical {111} planes. b, Cross-sections of the colloidal crystal along the \((\bar{1}10)\) plane (see coordinate system in a) demonstrate glide of a perfect dislocation \({\bf{b}}=\frac{1}{2}\left[110\right]\) in the [110] direction on a (001) plane. The order of the crystal layers is shown by the red and blue particles, located out of and into the view plane, respectively. Black lines show an extra half-plane. Scale bar, 20 μm (a).

We show here that colloidal crystals exhibit work hardening and that their normalized strength approaches the theoretical limit for materials and exceeds that of most atomic systems. The strength of atomic systems is set by the dislocation density; the maximum density is thought to be limited by the annihilation of nearby dislocations^41,42. The probability of this annihilation process strongly decreases with decreasing stacking fault energy^43,44. Hard-sphere colloidal crystals have vanishingly small stacking fault energy because of the lack of next-nearest-neighbour interactions. Annihilation of dislocations is not observed in our experiments, which may account for the very high dislocation density and, in turn, very high strength of these crystals. Moreover, we find that, after an initial transient, the relationship between the dislocation density and the strength of the colloidal crystals is in direct agreement with Taylor’s prediction for atomic systems, although hard-sphere interactions lack the complexity of atomic interactions. It is known that the specific details of the interatomic potential can affect, for example, the lattice resistance to the dislocation motion, which, in turn, explains why some atomic crystals break (brittle), whereas others deform plastically (ductile)^18,23. However, our work demonstrates that colloidal crystals follow the same universal behaviour of many ductile crystals: the exact interparticle interactions and the lattice resistance are of secondary importance to the interactions among dislocations. These measurements provide a new means to study crystal plasticity, as colloidal systems allow unprecedented real-time observation of dislocation dynamics that is inaccessible in atomic crystals. We provide direct experimental evidence that work hardening can be caused by the formation and destruction of sessile dislocation junctions. Although this is widely accepted, it has so far been supported only by numerical simulations^35,45,46 and indirect experimental evidence^20,47. Furthermore, the discrepancy between the Taylor equation and the measured flow stress during the transition from the early misfit dislocation configurations to those established by the shear highlights the importance of memory⁴⁸ and suggests that the deformation history is encoded in the structure of the dislocation network. These insights are essential for understanding the classic latent hardening experiments, during which different slip systems are activated successively⁴⁷. Our experiments highlight the competition of the different deformation processes—glide of mobile Shockley and glide of Lomer dislocations—at the limit when the flow stresses approach the theoretical limit of strength. Finally, the exhaustion of stacking faults through the motion of trailing partial dislocations is not unique to colloids but should also be important, for example, in the deformation of nanocrystalline materials⁴⁹, in which the stacking fault and sample sizes are similar. Observation of work hardening in colloidal crystals not only provides insights into this soft matter system but also provides an opportunity to gain important insights into the underlying mechanisms of work hardening itself.