Mathematicians have described1 a new class of shape that characterizes forms commonly found in nature — from the chambers in the iconic spiral shell of the nautilus to the way in which seeds pack into plants.
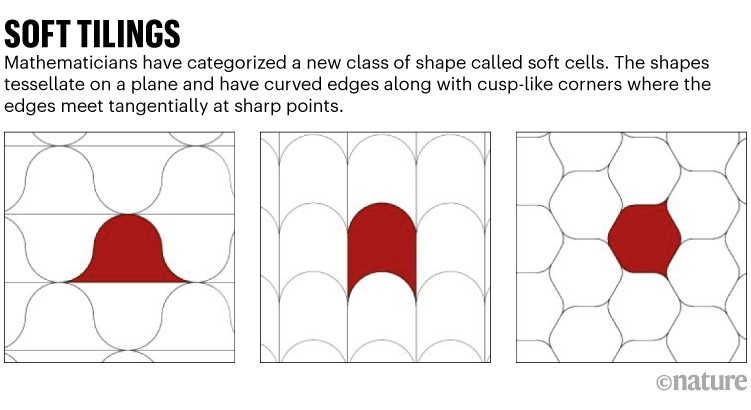
The work considers the mathematical concept of ‘tiling’: how shapes tessellate on a surface. The problem of filling a plane with identical tiles has been so thoroughly explored since antiquity that it’s tempting to suppose that there is nothing left to be discovered about it. But the researchers deduced the principles of tilings with a new set of geometric building blocks that have rounded corners, which they term ‘soft cells’.
‘Geometry can be very simple, but totally deep’: meet top maths prizewinner Claire Voisin
“Simply, no one has done this before”, says Chaim Goodman-Strauss, a mathematician at the National Museum of Mathematics in New York City, who was not involved in the work. “It’s really amazing how many basic things there are to consider.”
It has been known for millennia that only certain types of polygonal tile, such as squares or hexagons, can be packed together to fill 2D space with no gaps. Tilings that fill space without a regularly repeating arrangement, such as Penrose tilings, have attracted interest since the discovery of non-periodic structures called quasicrystals in the 1980s. Last year, the first quasiperiodic tiling, lacking any true periodicity, that uses just a single tile shape was announced by Goodman-Strauss and his colleagues2.
Source: Ref. 1
Avoiding corners
Mathematician Gábor Domokos at the Budapest University of Technology and Economics and his co-workers returned to periodic polygonal tilings — but considered what happens when some of the corners are rounded. In two dimensions, not all corners can be rounded without leaving gaps. But space-filling tilings become possible when some corners are deformed into ‘cusp shapes’. These corners have internal angles of zero — their edges meet tangentially as in a teardrop, and they fit snugly next to the rounded corners (see ‘Soft tilings’).
Domokos and colleagues devised an algorithm for smoothly converting geometric tiles — either 2D polygons or 3D polyhedra, like the bubbles of a foam — into soft cells, and explored the range of possible shapes these rules permit. In 2D, the options are fairly limited: all tiles must have at least two cusp-like corners. But in 3D, introducing softness has some surprises in store. In particular, these soft cells can fill volumetric space without having any corners at all.
The researchers devised a quantitative measure of the degree of ‘softness’ of such space-filling 3D tiles, and found that the softest are not compact shapes, but instead develop flange-like circular ‘wings’ at their edges, typically emerging from saddle-like tile surfaces. The softest shape elements are in fact circular discs, which the flanges of the 3D tiles approximate.
The cost of kinks
Domokos thinks that, for any given initial polyhedral tiling, there is a unique tiling with the greatest possible softness. He also suspects that, in real materials, this optimum will turn out to maximize some physical quantity related to, say, the bending energy in the edges or the interfacial tension. He admits that he and his colleagues currently have no proof of this maximal-softness conjecture, but hopes “that someone much smarter will pick this up and prove it”.
Source: Ref. 1
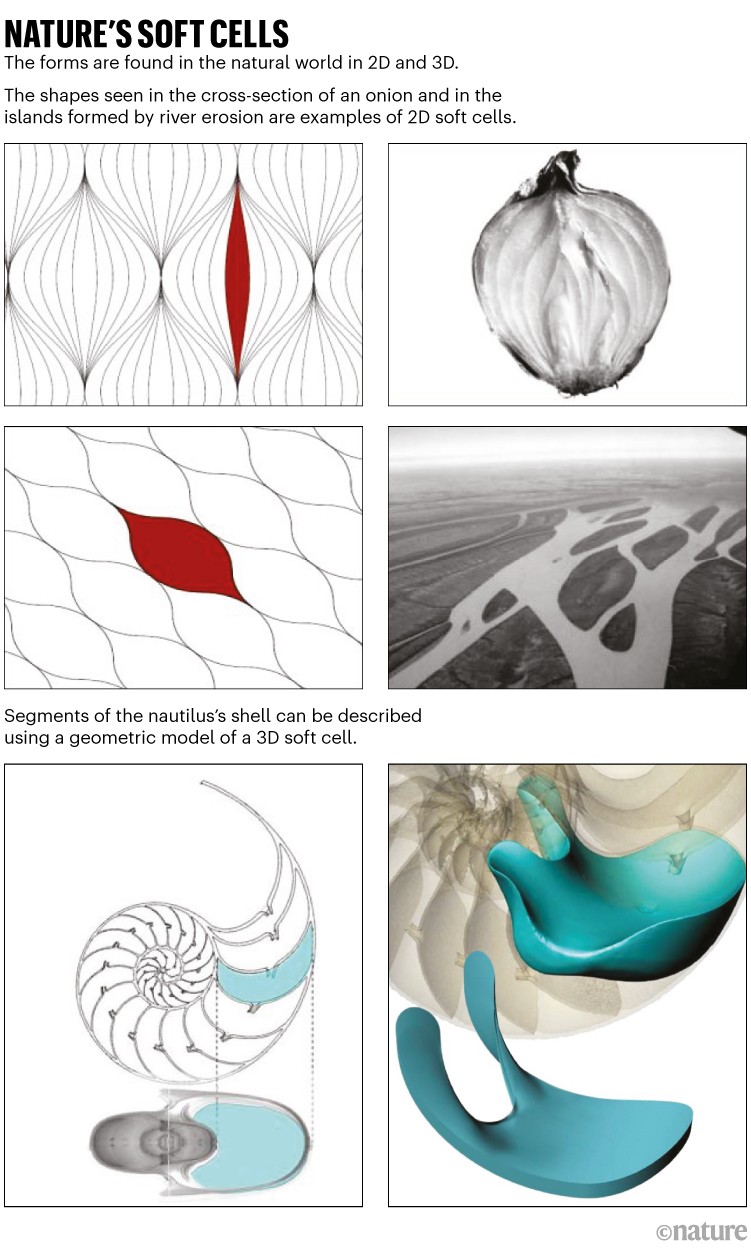
The researchers identified soft tilings in nature in the 2D shapes of islands in braided rivers, cross-sections of the concentric layers in an onion and biological cells in a tissue, as well as the 3D compartments of spiral shells such as those of the nautilus, a marine mollusc (see ‘Nature’s soft cells’). Nature generally seeks to avoid corners, they think, because such kinks have a high cost in deformation energy and can be sources of structural weakness.
Studying the nautilus “was the turning point” of the work, says Domokos. In cross-section, the shell compartments looked like 2D soft cells with two corners. But co-author Krisztina Regős, also at the Budapest University of Technology and Economics, suspected that the actual 3D chamber had no corners at all. “That sounded unbelievable,” says Domokos. “But later we found that she was right.”
Ancient geometry
Given that the analysis uses mathematics that has been known for centuries, it might seem surprising that no one has formalized the notion of soft cells until now. But Goodman-Strauss suspects that “the soft edges are enough of a block for geometers not to have thought about it” previously.
“The universe of polygonal and polyhedral tilings is so fascinating and rich that mathematicians did not need to expand their playground,” says Domokos. He suspects that there is a common perception that fresh insights demand advanced mathematics or cutting-edge computation, not simply well-established geometric methods.

The Heydar Aliyev Center in Baku was designed architect Zaha Hadid, whose buildings use soft cells to avoid or minimize corners.Credit: Mladen Antonov/AFP via Getty
Goodman-Strauss sees the work as offering “a kind of descriptive language of structure”, but which might not yet reveal new physical principles underlying the formation of such structures in nature. To understand, say, river banks, he says, it is probably still necessary to consider the physical process from first principles, such as the roles of flow, sediment transport and erosion.
Domokos and colleagues think that architects such as Zaha Hadid have long used soft cells intuitively to avoid or minimize corners, either for aesthetic or structural reasons. Since completing the paper, Domokos and co-author Alain Goriely of the University of Oxford, UK, have collaborated with architects at the California College of Arts in San Fransisco, who devised an award-winning structure using soft-cell elements made — appropriately — from eggshells.

